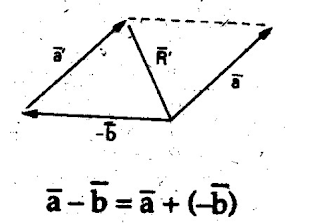Dalam fisika, terdapat dua jenis besaran yang digunakan untuk menggambarkan fenomena alam, yaitu besaran skalar dan besaran vektor. Meskipun keduanya memiliki peran penting, terdapat perbedaan mendasar antara keduanya.
Perbedaan Besaran Skalar dan Vektor
1. Besaran Skalar:
Besaran skalar adalah besaran yang hanya memiliki magnitudo (besar) saja, tanpa arah atau orientasi tertentu. Besaran ini dinyatakan dengan angka dan satuan yang sesuai. Contoh besaran skalar meliputi massa, suhu, volume, kecepatan, dan waktu. Ketika melakukan operasi matematika terhadap besaran skalar, kita hanya perlu memperhatikan perhitungan magnitudo tanpa memperhatikan arahnya. Misalnya, jika kita menjumlahkan dua besaran skalar seperti panjang 5 meter dengan panjang 3 meter, hasilnya akan menjadi 8 meter.
2. Besaran Vektor:
Besaran vektor adalah besaran yang memiliki magnitudo (besar) dan arah atau orientasi tertentu. Besaran ini dinyatakan dengan angka, satuan, dan arah yang sesuai. Contoh besaran vektor meliputi percepatan, gaya, kecepatan, dan momen. Ketika melakukan operasi matematika terhadap besaran vektor, kita harus memperhatikan kedua komponennya, yaitu magnitudo dan arah. Misalnya, jika kita menjumlahkan dua besaran vektor seperti gaya 5 Newton ke arah timur dengan gaya 3 Newton ke arah utara, kita harus menggabungkan kedua vektor tersebut secara vektorial untuk mendapatkan hasil yang benar.
Secara garis besar:
Contoh : jumlah siswa di dalam kelas, harga sebuah rumah, massa, waktu, volume,
suhu, massa jenis.
Contoh: perpindahan, kecepatan, percepatan, gaya, momentum.
Untuk besaran vektor diberi lambang anak panah. Panjang anak panah menyatakan besar vektor dan arah anak panah menunjukkan arah vektor.
Perhitungan Vektor
Penjumlahan Vektor
1. Metode Poligon atau Grafis
Penjumlahan dari beberapa vekor menghasilkan resultan. Resultan diperoleh dengan menggambarkan anak panah-anak panah vektor secara sambungmenyambung
dengan memperhatikan panjang (besar atau nilai) maupun arah anak panah yang bersangkutan. Ekor anak panah yang satu dihimpitkan pd ujung
anak panah yang mendahuluinya. Selanjutnya resultan merupakan anak panah yang menghubungkan titik pertama vektor dan titik terkhir penjumlahan vektor.
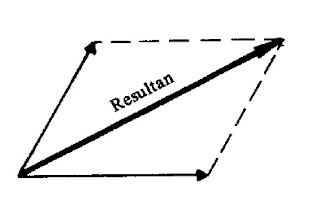
2. Metode Jajaran Genjang
Metode ini berguna untuk menjumlahkan dua buah vektor: Resultan dua vektor yang berpotongan adalah diagonal jajaran genjang dengan kedua vektor tersebut sebagai sisi jajaran genjang. Arah Resultan adalah menjauhi titik awal kedua vektor.
Pengurangan Vektor
Jika Vektor B dikurangkan dari Vektor A, maka dilakukan dengan cara membalikkan arah B dan jumlahkan terhadap vektor A, sehingga A – B = A + (-B)
Penjumlahan dan Pengurangan Vektor dengan fungsi Trigonometri
Diperoleh dengan memperhatikan segi tiga siku-siku.
Fungsi-fungsi ini kerap digunakan dalam bentuk:
O = h. sin θ a = h. cos θ o = a tan θ
Penjumlahan komponen Vektor : Penjumlahan beberapa vektor didapat dengan menjumlahkan komponen-komponennya; setiap vektor diuraikan menjadi komponen x, y dan z. Maka komponen Rx vektor resultan adalah jumlah aljabar semua komponen x, demikian pula komponen Ry dan komponen Rz vektor resultan, maka besar vektor resultan R adalah:
Perkalian Vektor
Ada dua cara untuk mengalikan dua vektor:
1. Perkalian Skalar antar dua vektor (DotProduct = Perkalian Titik).
Contoh: W = F. s dimana: F dan s adalah vektor bersudut apit 0º, W adalah skalar
2. Perkalian Vektor antar dua vektor (Cross Product = Perkalian Silang).
VEKTOR SATUAN: i, j dan k masing-masing ditetapkan terhadap sumbu-sumbu x, y dan z.
Vektor F pada gambar ditulis:
F = 3i + 5j + 4k
Vektor F mempunyai komponen di sumbu x = 3 satuan, di sumbu y = 5 satuan, dan di sumbu z = 4 satuan.
Contoh Penjumlahan dan Pengurangan vektor satuan
F1 = 4i + 3j
F2 = 8i + 2j + 3k
1. F1 + F2 = (4+8)i + (3+2)j + (0+3)k = 12i + 5j + 3k
2. F1 – F2 = (4-8)i + (3-2)j + (0-3)k
= -4i + j – 3k
3. F2 – F1 = 4i – j + 3k
Penutup dan Kesimpulan
Dalam artikel ini, kita telah membahas perbedaan mendasar antara besaran skalar dan vektor, serta signifikansinya dalam pemahaman kita tentang fisika dan matematika. Besaran skalar adalah besaran yang hanya memiliki magnitudo atau nilai numerik, sedangkan vektor adalah besaran yang memiliki magnitudo dan arah.
Perbedaan ini memiliki implikasi yang penting dalam berbagai konteks. Dalam fisika, vektor digunakan untuk menggambarkan pergerakan dan interaksi benda-benda dalam tiga dimensi. Kecepatan, percepatan, gaya, dan momentum adalah contoh besaran vektor yang penting dalam fisika. Dengan menggabungkan magnitudo dan arah, vektor memungkinkan kita untuk melakukan perhitungan yang lebih kompleks dan mendapatkan pemahaman yang lebih lengkap tentang pergerakan benda.
Di sisi lain, besaran skalar digunakan untuk mengukur besaran yang tidak memiliki arah atau orientasi tertentu. Contoh besaran skalar termasuk massa, panjang, suhu, dan waktu. Besaran skalar digunakan dalam banyak bidang, baik dalam ilmu alam, ekonomi, atau sains sosial, di mana hanya nilai numerik yang relevan dalam perhitungan atau analisis.
Dalam matematika, perbedaan antara besaran skalar dan vektor juga penting. Vektor dapat ditambahkan atau dikurangi menggunakan operasi vektor, sedangkan besaran skalar dapat dikalikan atau dibagi dengan skalar. Operasi vektor memungkinkan kita untuk memodelkan pergerakan dan transformasi geometri dalam ruang.
Dalam penutup, perbedaan antara besaran skalar dan vektor memainkan peran yang signifikan dalam pemahaman kita tentang fisika dan matematika. Memahami perbedaan ini memungkinkan kita untuk mengaplikasikan konsep-konsep ini dengan tepat dalam analisis dan pemecahan masalah. Besaran skalar dan vektor saling melengkapi dalam memberikan gambaran yang lebih lengkap tentang fenomena alam dan dunia yang kompleks di sekitar kita.
Dengan menghargai perbedaan besaran skalar dan vektor, kita dapat memperluas pemahaman kita tentang sifat dan karakteristik besaran-besaran ini, dan menggunakannya dengan bijaksana dalam berbagai konteks ilmiah dan matematika.
Mau donasi lewat mana?
Donate with PaypalGopay-