Internal reactions and methods of sections- for bars, beams and cables

Internal reactions and methods of sections are commonly used in the analysis of structures such as bars, beams, and cables. These methods involve breaking down a structure into smaller sections to analyze the internal forces and moments that act on it.

Internal reactions refer to the forces and moments that are developed within a structure as a result of external loads or applied forces. These internal reactions can be tension, compression, shear, bending, or torsion forces, depending on the type of structure being analyzed.

Methods of sections involve cutting a section through a structure and analyzing the internal reactions within that section. This method is used to determine the internal forces and moments within a structure and can be used to calculate the stress and strain within different sections of the structure.

For bars, internal reactions are typically simple, with tension and compression being the primary internal forces. The method of sections for bars involves cutting a section through the bar and analyzing the internal forces and moments within that section. This method can be used to determine the stress and strain within different sections of the bar.

For beams, internal reactions can be more complex, with bending and shear forces being the primary internal forces. The method of sections for beams involves cutting a section through the beam and analyzing the internal forces and moments within that section. This method can be used to determine the bending moment, shear force, and deflection of the beam.

For cables, internal reactions are primarily tension forces. The method of sections for cables involves cutting a section through the cable and analyzing the internal forces and moments within that section. This method can be used to determine the tension force and sag of the cable.

Overall, internal reactions and methods of sections are important tools in the analysis of structures and can provide valuable information about the internal forces and moments that act on a structure.

Internal reactions and methods of sections- for bars, beams and cables

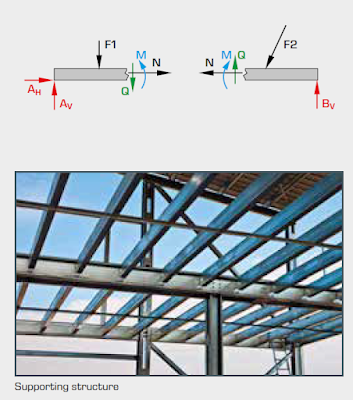
The support structures are composed of different structural supporting elements. The supporting elements are divided into one-dimensional (bar or beam), two-dimensional (plate or disk) and three-dimensional elements (solid-supporting structure).

To investigate internal reactions in components or mechanical systems, these are reduced to a few important properties through modelling. Geometric idealisation then eliminates seemingly insignificant dimensions.

Instead of three-dimensional supporting elements, two-dimensional supporting elements/plane-supporting structures (plates, disks and frames) and one-dimensional supporting elements/linear structures (beams, bars, arches and cables) are considered. In this chapter, we look at one-dimensional supporting structural elements.

One-dimensional supporting elements

Bar: A support element, flexibly mounted at both ends, which can transfer tensile and compressive forces along the bar axis. Depending on whether a bar transfers tensile or compressive forces, it is referred to as a tension bar or a compression bar.

Beam: Rectilinear supporting element that can transfer forces along its axis, transverse to its axis and moments. Horizontal elements are generally known as beams or girder and vertical elements are known as pillars or columns.

Cable: A support element that can only transfer tensile forces. A cable that is attached at two defined points is the equivalent of a tension bar.

Note:

F forces,
M bending moment,
A, B support forces

Internal forces

Using notional sections, parts are cut out of the support structure, which is in equilibrium. To maintain equilibrium, the internal reactions, also known as section reactions or internal forces, are entered into the sections. In statics, the internal reactions show the forces and moments within a component as a reaction to the action of the external forces.

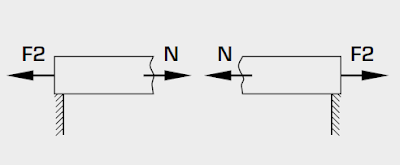
Normal force

The normal force runs in the direction of the beam axis. This force causes a change in the beam length through an internal reaction to tensile or compressive external forces acting on the beam.

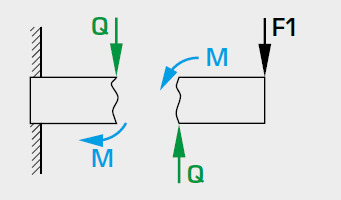
Shear force

The shear force is perpendicular to the normal force. This force results in shear deformation and is the beam’s internal reaction to the acting transversal forces.

Bending moment

The bending moment runs around the centroid of the section. This moment causes the beam to bend as a reaction to (tensile and compressive) forces acting on the beam from the outside

Nonte:

F1 force,
F2 tensile force,
M bending moment,
N normal force,
Q shear force

Free-body diagrams are the main method to represent the internal force states in bars, beams and cables. For beam-structures in particular, free-body diagrams are used to characterise the internal stress state and, consequently, are used when dimensioning the beam.

Considering the internal forces is a prerequisite for calculating deformation and investigating the load-bearing capacity of materials as a measure of their strength. When designing components, the internal forces provide the designer with the crucial indicators for necessary dimensions or the type of load distribution.

Internal reactions

1. The studied bodies or mechanical systems are removed from the environment through representation in the free-body diagram.

2. All forces acting on the body or system are determined. Especially where the body or the mechanical system under investigation is separated from adjacent bodies. Since the internal forces change between the different cross-sections, we plot their curves for a better overview. The shear force, normal force and bending moment are represented as areas.

3. Unknown forces are calculated using the equilibrium conditions.